大学数学必备基础公式汇总

大学数学的基础公式有哪些

在这里，我将与您分享一些大学食品的基本公式。
1。
三角函数基于角度（数学，最常用的弧度，下面相同）与自变量，角度对应于点点或其条件的任何角度和单位的末端的函数是变量的函数。
三角函数和特殊角度的三角函数的值表。
2。
差角公式与差分三角函数之间的差异（也称为三角形函数的减法定理）是（不同的）三角函数的三角函数的几个角度。
三角函数的第三个三重态公式。
三角函数双角度公式是用角度的三角形函数表达两倍的角度的三角函数。
4。
微型计算是与较高数学中的概念和应用有关的分支，点和数学分支。
5。
拱形区域的计算公式。
弓形区域的公式是风扇形区域 - 三角形区域。

数学公式

大量的中学和高中的数学公式和定理（仅参考）1。
有一个直线，只有两个点2分2。
两个点之间的最短段3。
同等角度或相等角度的补充角度 是等于4。
一致或相等角度相等的补充角度相等5。
有一个直线，只有一条直线垂直于已知的直线。
6。
在连接上面点的所有线段之间的直线和直线之外的一个点，垂直段最短。
7平行的公理，穿过直线外的一个点，有一个直线与这条直线平行。
8如果两条直线平行于第三条直线，则这两条直线也彼此平行。
9相同位置的角度相等，两条直线平行。
10内部偏差角相等。
两条直线是平行的。
同一侧的11个内部角度是互补的。
两条直线是平行的。
12两条直线是平行的。
同心角度相等。
13两条直线是平行的。
内角相等。
14两条直线是平行的。
同一侧的内部角度是互补的。
15定理三角形的两个侧的总和大于第三侧。
16三角形的两个侧之间的差异小于第三侧1 7三角定理的内部角度的总和。
三角形的三个内部角度的总和等于180°18推论1两个急性角度。
右三角形是互补的19推论2三角形的外部角度等于两个不毗邻的内部角度的总和。
一致三角形的内部角度为21。
相应的侧面和相应的角度相等。
22。
侧角侧公理（SAS）。
如果有两个侧面，并且其中的角度相等，则两个三角形是一致的。
23。
角侧公理（ASA）有两个角度及其角度。
两个三角形的侧面对应于相等的三角形是一致的24推论（a as），有两个角度，两个角度，其中一个角度的相对侧与一致性相对应。
25个侧面是一致的。
公理（SSS）有三个侧面对应于两个三角形的侧面。
26.斜角和直角公理（HL）有斜边。
两个与右侧相对应的右三角形是一致的27定理1距角度与角度两侧的角度的距离的距离相等28个定理2 A点与角度两侧的距离相同 在角度29的三角形上，角度的一分为双方是距角度两侧的距离。
所有点等于30属性三角形定理的属性的集合的距离三个属性三角形等级三个角度相等的两个基础角度相等（也就是 ，等边角相等）31推论1等化等质三角形的顶点角度的一分为二，底座垂直于底座32等质等离子三角形三角形的角度的三角形，底座上的中线和高度 碱基彼此一致33推论3等于等边三角形的角度相等，并且每个角度等于60°34等同进三角形的测定定理，如果三角形的两个角度等于两个角度，则是两个角度相反的角度。
也等于（等于均等的边）35推论1所有三个角度都相等。
三角形是等边三角形36推论2等于60°的角度等于60°A等于三角形的三角形是右三角形的等边三角形37，如果急性角度，则 等于30°，那么它对立的右侧等于斜边38右三角形的斜边的中线等于斜边39个定理线段的一半是垂直的，垂直于双分配器上的点，该线段的两端段之间的距离等于。
40逆定理和距线段两个端点相同距离的点位于线段的垂直分配器上。
41线段的垂直一分配器被视为所有点的集合，等于线段的两个端点之间的距离。
42对称直线对称的定理1TWO数字是一致的形状43定理2，如果两个数字在直线上是对称的，那么对称的轴是连接相应点的线的垂直分配器。
44定理3如果两个图是关于直线的对称的，如果它们的相应线段或延伸线相交，则相交点在对称的轴上。
上面45的匡威定理如果两个数字之间的对应关系连接点的线是通过相同的直线垂直划分的，则两个数字对这条直线46毕达哥拉斯定理对称是对称的。
右三角形的侧a和b等于斜边C的平方，即A^2+b^2 = C^247毕达哥拉斯定理的相反定理。
如果三角形的三个侧面很长，则a，b和c a^2+b^2 = c^2之间存在关系，那么此三角形是右三角形48定理，四边形的内角的总和是 等于360°49，四边形的外部角度的总和等于360°50，多边形定理n-gon的内角和内部角度的总和等于（n-2）×1 80 °51推断任何多边形的外角之和等于360°52平行四边形特性定理1平行四边形的相反角度等于53平行四边形属性定理2平行四边形的相反侧等于54个平行线段 夹在两条平行线之间的夹在55平行四边形质量定理3平行四边形一分分彼此的对角线彼此的对角线56平行四边形确定定理1 a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a imateragilogragram均衡图57平行四边形确定定理2二次。
相等的相对侧​​是平行四边形58平行图定理3对角线。
四边形四边形是平行四边形59平行四边形判断定理4一组平行平行的平行平行四边形60矩形自然定理。
矩形判断定理1。
矩形63矩形判断定理的四边形角的三个角落。
并且每条对角线分为一组对角线66钻石面积=对角乘数的一半，即S =（a×b）÷267钻石形测定定理1等于菱形68钻石的四个侧 - 形状的判断定理2对，角线的平行线为钻石形状的69平方自然定理1正方形的四个角度是正确的角度，而70平方形的特性定理2 fangxian 2斜线是70平方属性的四个侧面 关于中央对称性的两个图形的相等线路分区一组分区71定理1是关于中央对称性的两个图形的72定理2。
对称点是对称的，线是对称的。
图形的相应点通过特定点并将其除以此点，然后在同一底部的其他腰部定理和其他腰部定理和其他腰部梯形。
两条对角线，例如两者的76 Cascado测定定理在同一底部的角度，梯形等于腰围77颗粒状梯形。
在直线上截获的线段相等，然后在其他直线上截获的线段也等于79参考1梯形腰部的中心平行于底线，将其分为 另一个腰。
平行于另一侧的直线分为第三侧的81三角形的第三侧的第三侧。
，等于两个底部的一半l =（a+b）÷2s = l×h83（1）如果a：b = c：d，则比率的基本性质，那么ad = bc，如果ad = bc， 然后a：b = c：dwc ∕/ s∕？ 84（2）如果a/b = c/d，则比较的性质，则（a±b）/b =（c±d）/d85（3），如果a/b = c/d = = m / n（b+d+ +n≠0），然后（a+c+…+m） /（b+d+ +n）比例定理三平行线切开两条直线。
（或两侧的延伸线）相应的线是成比例的，然后该直线平行于三角形89平行于三角形，而直线与另一侧相交。
90定理三个边的三个侧面的三角形与三角形的直线平行，并与其他两个侧（或两侧的延伸）相交。
）92右角三角形分为两个右角三角形，高高除以斜面边缘的高度。
三角形相似（SSS）95定理如果右角三角形和右角边缘与另一个右边的 - 角三角形和右边缘的倾斜边缘成比例，则这两个右三角形与96相似。
比较，与相应的角线比相比，该比率等于97自然定理。
它等于其剩余角度的残留弦值，任何锐角的剩余弦值等于100号角的剩余角度的正弦值。
任何锐角的正切值等于 其剩余角度的剩余剪切值。
正切值101是固定点距离，等于固定长度点集102。
内部可以被视为小于半径的103发子弹的集合。
从105到固定点的距离等于相同的圆或等待。
以及已知线段的两个端点。
它是线段107至已知角度的垂直分配器。
该点的轨迹两侧之间的距离是角度108的三角形的基因座到两个平行线相距的点。
它是平行于两个平行线的直线和等距。
109定理的三个未在同一直线上的三个点确定一个圆。
。
110垂直直径的定理直径垂直于字符串将弦分为一分为一分为二，并将两根弧形由字符串划分的两个弧线。
111推论1 conterary1①垂直于弦的和弦的直径（而不是直径），并将两个弧形由和弦缩减。
②字符串的垂直度。
双层子穿过圆的中心，并将和弦分配两个弧形③将和弦均匀的弧形的直径分配，将和弦垂直于垂直，并将另一个弧形由和弦划分为和弦112 Corollary 2 arc由两个平行2平行于弧线。
一个圆的和弦相等113，一个圆圈具有圆的中心，作为其对称定理的中心114的中央对称人物的114中心，以一致或相等的圆圈为准，以相等的中心角度尺寸相等的弧线相等，它们对立的和弦相等，并且相等，并且是相等的，并且 和弦及其中心之间的距离相等。
在同一圆圈或一致圆圈中的115个推论，如果两个中心角，两个弧，两个和弦或两个字符串的和弦中心距离中的一组数量相等，那么与它们相对应的剩余数量集相等116个定理，由ARC绕的圆周角度为116 等于圆的中心角的一半，它缩减为117推论1圆角由相同的弧或相等的弧相等。
在相同或相等的圆中以相等的圆角亚倾斜的弧线也等于118推论2圆形由半圆（或直径）圆周角来缩减的圆是直角； 由90°圆周角来缩写的和弦是直径为119推论3，如果三角形的一侧的中线等于这一侧的一半，则三角形是右三角形的120个定理，一个刻有圆圈的对角线的对角线 是互补的，任何外部角度等于121①直线l，而⊙o相交d r r②直线l，切线d = r d = r直线l和直线l，⊙ 切线线穿过半径的外端，垂直于这条直线半径的直线与圆形123属性定理相切。
圆的切线线垂直于穿过切线124循环点1的半径。
穿过圆的中心并垂直于切线，必须穿过切线125推论2一条直线穿过切线和垂直于切线的直线必须穿过圆的中心126个切尔姆的中心126个切线的切线。
在圆形外部两个切线引导圆的外部，其切线的长度相等，连接圆的中心的线和两个切线之间的角度划分的角度127圆圈的两个相对侧的两个相对侧的总和。
是等于128的弦切角定理，弦切角等于一对弧度，如果两个和弦切线所包含的弧线等于等于圆的圆角的129 corlrolary，则这两个和弦角度的切线是，那么这两个和弦的切线是 也相等。
130与两个相交和弦相交的和弦定理，在一个圆圈中，两条线段的长度的产物除以交点分配。
131推论如果和弦垂直于直径相交，则和弦的一半是将直径为1 32切割线形成的两个线段的中间项分开 圆圈外的一个点。
切线线的长度是从这个点到割线线和圆的相交的两个线段的长度比的中间项。
133。
推论：从圆外的一个点绘制了两个割线。
从此点到每个割线线和圆的交点的两个线段的长度的乘积如果两个圆圈是切线的，则圆相等134，则切线必须在连接中心线上。
135①两个圆圈由d r+r限制在d = r+r的范围内，两个圆圈绕过两个圆圈r-r-r-r r-r r ＜d r+r+r+r（r r r r r r r） - 两个圆圈是d = r-r （r＞r）两个圆圈刻有d r-r-r（r r r）136定理，连接两个圆的中心的线相交，并将两个圆圈的共同 *垂直于137定理分为N≥3337（n≥3333） ）：⑴通过序列连接点获得的多边形是圆的内部连接常规的N侧多边形（2），并通过每个点绘制圆的切线线，因此，一个多边形的多边形，其顶点是相邻的交叉点 切线线是对该圆圈的常规n gon。
138定理：任何常规多边形都有外接圆和内切圆。
这两个圆是同心圆。
139 每个正n边形的内角等于(n-2)×180°/n1 40 定理 正n边形的半径和边心距 将正n边形分成2n个全等的直角三角形 141 正n边多边形的面积 Sn=pnrn/2p 表示正n边多边形的周长 142 正n边多边形的面积 n 边多边形 √ 3a/4a 表示边长为 143，如果一个正 n 边多边形围绕一个顶点有 k 个角。
由于这些角度之和应为 360°，则 k×(n-2)180°/n=360° 变为 (n-2)(k-2 )=4144 弧长计算公式：L=n兀R／18014 5扇形面积公式：S扇形=n兀R^2/360=LR/2146 内公切线长度=d-(R-r) 外公切线长度=d-(R+r) （还有其他的，请帮忙补充） 实用工具：常用数学公式分类公式表 法理分解过程中，A^2-B^2 = (A+B) (A-B) A^3+ B^3 = (A+B) (a^2-AB+B^2) A^A^ 3-B^3 = (A-B (A^2+AB+B^2) 不同三角形。
< => -B ≤A ≤b | ≥ | A | A ≤ A | A 的解 B^2-4AC)/2A 根 系数之间的关系 x1+x2 = -b/ax1*x2 = c/a 注：伟达定理 B^2-4AC = 0 注：有两个 方程：有两个方程 等实根 B^2-4ac> 0 注：方程有两个实根 (A+B) = sinacosb+cosasinbsin (A-B) = sinacosb-sinbcosa cos (A+B) =。
COS ACOSB-SINASINBCOS (A-B) = cosacosb+sinasinbtan (A+B) = (TANA+TANB)/(1)/(1)/(1) -tanatanb ) tan (a-b) = (tana-tanb)/(1+tanatanb) COT (a+B) = (Cotacotb-)/(COTB +科塔）。
cota) 除法公式 TAN2A = 2TANA/[1- (TANA)^2] cos2a = (cosa)^2- (Sina)^2 = 2 (COSA)^2-1-2 (SINA)^2 半角公式 sin (a/2) = √ ((1-cosa)/2) sin (a/2) =-√ ((1-cosa)/2) cos (a/2) = √ ((1+cosa)/ 2) COS (A/2) =-√ ((1+cosa)/2) tan (a/2) = √ ((1-cosa)/((1+cosa)) tan (a/2) =- √ ((1-COSA)/((1+COSA)) COT (A/2) = √ ((1+cosa)/((1-cosa)) COT (a/2) =-√ ((1+ (1+ 1+ (1+) COSA)/((1-COSA))。
微分累加 2sinacosb = sin (a+b)+sin (a-b) 2 cosasinb = sin (a+b) -sin (a-b)) 2COSACOSB = cos (A+B) -sin (a-B) -2SinaSinb = cos (A+B) -COS (A-B) Sina+SINB = 2sin ((A+B)/2) COS ((A-B)/2COSA+COSB = 2COS ((A+B)) /2) SIN ((A-B)/2) TANA+TANB = SIN (A +B)/COSACOSB 之前的一些 N 和 1+2+3+4+5+6+7+8+9+ n (n+1)/21+3+5+7+9+11+13+15+…+(2N-) = n2 2+4+6+8+10+12+14+…+(2N ) = n (n+1) 51^2+2^2+3^2+4^2+5^2+6^2+7^2+ +n^2 = n (N+1) (2N+1)/61^3+2^3+3+4^3+5^3+6^3+ n^3 = n2 (n+1) 2/41** 2+2* 3+3*4+4*5+5*6+6*7+ +n (n+1) = n (n+1) (n+2)/3 正弦定理 A/Sina = B/ sinb = c/sinc = 2R 注：R，其中R代表三角形外圆半径，定理B^2 = A^2+C^2-2accosb 注：角B为边A与C-C边C的角圆标准方程（x-a )^2+(y-b)^2 =^r2 注：(A, B)为圆心坐标圆的一般方程 x^2+y^2+dx+ey+f = 0 注：D^2 2 +E^2-4F> 0 抛物线 标准方程 y^2 = 2pxy^2 = -2pxy^2 = 2pyx^2 = -2py 直棱镜边面积 s = c*h 斜边边面积 s = c ' *h 正棱锥的侧面面积 s = 1/2c*H '正棱锥的侧面面积 S = 1/2 (c+c') h '圆桌边线面积 s = 1/2 (c+c') l = pi (R+R ) L球的表面积 s = 4pi*R2 圆柱边线 s = c*h = 2pi*h 圆锥边面积 s = 1/2*c*l = pi*r*L 弧长公式 L = a*ra 是圆心心 角的弧数 R>0 扇形面积公式 s = 1/2*L*r 圆锥体积公式 V = 1/3*s*h 竞赛体积公式 V = 1/3*pi*r2h。
= S'L 注：其中，S'为直截面积，L为侧边长柱体积的体积公式 V = S*H 圆柱 v = Pi*R2H

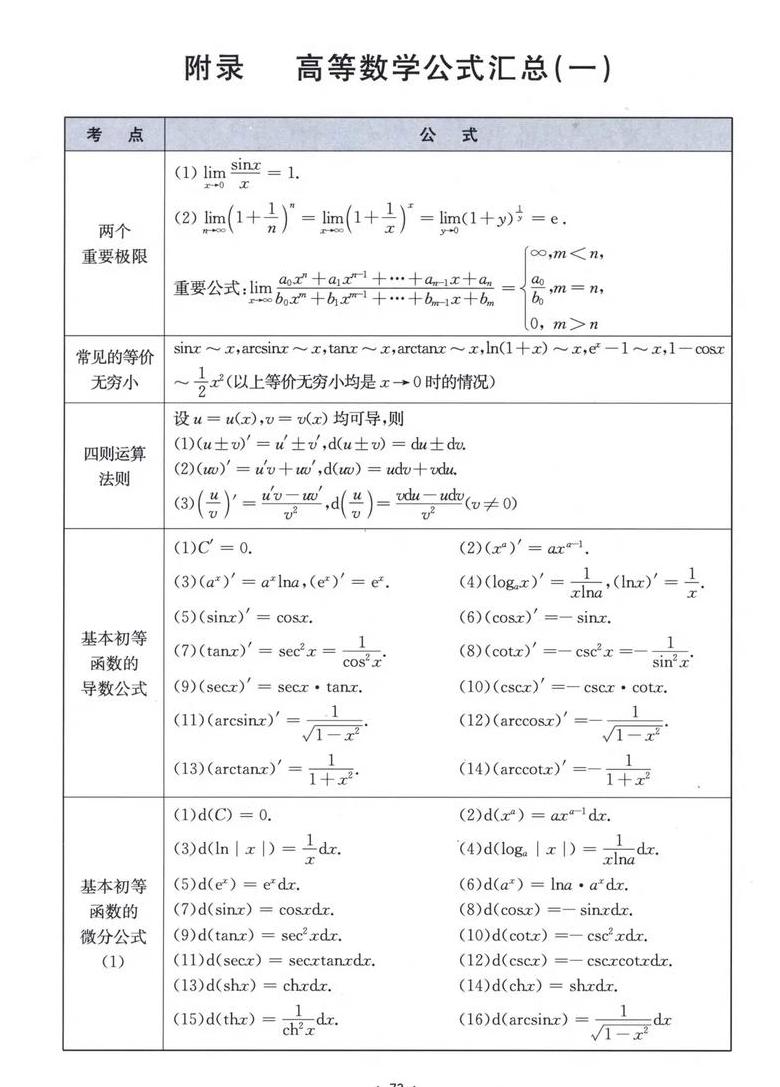
大学高等数学常用的初等函数泰勒公式有哪些，求总结

e^x = 1+x+x^2/2!+x^3/3!+ +x^n/n!+ ln (1+x) = x-x^2/2+x ^3 /3- +(-1)^(K-1)*(x^k)/k (| x | <1) sinx = x-x^3/3!+X^5/5!- ---------------------- + (-1)^(k-1)*(x^(2k-1))/(2k-1)!+ (-∞ 1*3/(2*4)*x^5/5+ (| x |

数学有那些公式

1。
Fangxianc -week长度S面积A侧长=边缘长度×4C = 4A区域=边缘长度×边线S = A×A2，平方体V：体积长度表面积=边缘长度×边缘长度×边缘长度×6S×6S桌子 = a×a×6卷=边长×边缘长度×边缘长度v = a×a×a3，矩形c周长s面积a侧长=（长+宽度）×2c = 2（a+b（a+b（a+） b）面积=长度×宽度s = ab4，文化V：音量S：区域A：长B：宽度H：高度（1）表面积（长度×宽+宽+长×高×高宽×宽度×高度）×2S = 2（ AB+（AB+AH+BH）（2）体积=长度×宽度×高度V = ABH5三角形S面积A高面积=底部×高度÷2S = AH÷2 Triangle高=区域×2÷底部三角形底部=面积=面积×2 ÷高6平行的Sidaming s面积A底部H高面积=底部×高度S = AH7梯形S区域A底部底部底部h高面积=（底部+底部+底部）×高高÷2s =（A+B）×H÷ ÷28圆形S面积C周长∏D =直径r =半径（1）周长=直径×= 2××半径c = ∏D = 2∏R（2）= 2∏R（2）=半径×半径×半径×9圆柱v ：卷H：高s； 底部区域R：底部半径C：底部长度（1）侧面区域=底部长度×高度（2）表面积=侧面区域+底部面积×2（3）音量=底部=底部=底部=底部×高度（4）体积=侧面=侧面 面积÷2×半径10锥V：音量H：高s； 底部区域R：底部半径卷=底部区域÷3总数=总数和差异问题公式（和 +差异）÷2 =大数字（和-Difference）÷2 =十进制和多个问题和÷（多数号-1 ）=十进制十进制×多数=大数（或-DECIMAL =大数）差异时间。
问题差÷（次-1）=十进制十进制×多重=大数（或十进制 +差异=差异=大数）植物问题1非裂口线种植问题可以分为以下三种情况：⑴如果您在 不截断的线必须种植树的两端，然后：植物数=段落数量 + 1 =全长÷植物间距-1全长=植物间距×（数字-1）植物间距=全长度÷（数字） 植物-1）。
，另一端，请勿种植树木，然后：植物数=段落数=全长÷植物间距全长=植物间距×植物间距=全长÷植物数量。
如果您不在非裂缝线的两端种植树，则植物数量=段数-1 =全长÷植物间距-1全长=植物间距×植物+1）植物间距 =全长÷（植物数量+1）2封闭线上种植问题的数量如下=段落数=总长度÷植物间距全长=全长=植物间距×植物的植物菌株间距= 全长长÷植物数量（利润 +损失）÷两个分布之间的差异=分布的各个部分（大利润-small利润）÷这两个分配之间的差异=参与分布数（大损失很大） - 小损失小损失）÷两个分布之间的差异=相遇数量涉及的分布=速度和×遇到时间时遇到时间÷速度和速度和速度=遇到时间÷遭遇时间追逐距离 =速度差×追逐时间追求时间=追逐距离÷速度差速度差=追踪距离÷chasing时间流量问题平滑流速=静态水速 +水流速度反向流量=静态水上速度 - 水电流速度 - 水电流速度水速度速度= （平稳流​​速 +反向流速）÷2水流速度=（平滑速度 - 反向流速）÷2浓度问题溶质溶质 +溶剂的重量=溶液的重量÷溶液的重量 ×100％=浓度溶液的重量×浓度=解决方案重量÷浓度÷浓度;浓度÷浓度的浓度÷浓度=解决方案利润的折扣=销售价格 - 成本利润率=利润÷成本×100％=（卖出价格÷成本 - 成本 - 成本 - 1）×100％上升和下跌金额=本金×上升和下降百分比折扣=实际价格÷原始价格×100％（折扣<1）利息=本金×利率×利率×税后税后税=本金=本金×时间×时间×（1 -20％）长度单位转换1 km = 1000米1米1米1米= 10分钟= 10分钟1分钟= 10 cm 1米= 100 cm 1 cm = 10 mm面积单位转换1平方公里= 100公顷1公顷1公顷 = 10000平方米1平方米= 100平方米，1平方米，1平方米= 100米= 100平方米1平方厘米1平方厘米= 100平方毫米（公差）累积单位1立方米= 1000立方米，1立方米，1立方米，1立方米， 1立方米，1立方米，1升，1立方厘米= 1 ml 1立方米= 1000浮雕单位转换1吨= 1000 kg 1 kg 1 kg = 1000g 1 kg = 1 kg = 1 kg rmb单位转换1元= 10 yuan = 10 角度和1元，1元= 100点时间单位转换1世纪DA月亮（31天）有：1 \ 3 \ 5 \ 7 \ 7 \ 8 \ 8 \ 10 \ 12月xiaoyue（30天）：4 \ 6 \ 6 \ 9 \ 11月28日 每天，每年2月29日，一年中的365天，年份的366天1天= 24小时1钟= 60分钟1点1分= 60秒= 3600秒= 3600秒的小学数学几何体长面积计算 一级方程式，矩形周长=（长度（长度 +宽度）×2c =（a +b）×22，平方长度=边缘长度×4C = 4A3，矩形的面积 square - volume =边长×边缘长度s = a.a = a5，三角形的面积=底部×高度÷2s = ah÷26，平行quadritar的面积=底部×底部×高度s = ah7底部）× 高度÷2s =（a + b）h÷28，直径=半径×2d = 2r半径=直径÷2r = d÷29，圆周×直径×直径=圆速率×radius×2c =2πr10，该面积 圆=圆速率×半径×半径定义定理三角形的定理公式=底部×高度÷2。
公式s = a×h÷2建立面积=边缘长度×边缘长度×边缘长度s = a = a× A矩形区域=长度×宽度公式s = a×b平行四边形面积=底部×高公式s = a×h梯形=（底部+底部+底部）×高度÷2 formula s =（a +b）h÷2内角和：三角形的内角和= 180度。
立方体的体积=长度×宽度×高公式：V = ABH矩形（或平方）体积=底部面积×高公式：V = ABH正方形尺寸=边缘长度=边缘长度×边缘长度×边缘长度：V = AAA圆 工资长度=直径×π公式：l =πd=2πr圆面积=半径×半径×半径×π公式：s =πr2圆柱形表面（侧）面积：圆柱柱的表面（侧面）面积等于 底部表面的高度高。
公式：S = CH =πDH=2πRH圆柱体的表面积：圆柱体的表面积等于底部表面的周长，加上两端的面积。
公式：S = CH+2S = CH+2πR2圆柱体积：圆柱体的体积等于底部区域的底部区域。
公式：v = sh锥体积= 1/3底部×累积高。
公式：V = 1/3SH分数的加法和减法：添加并减去同一分母的分数，并且仅添加分子并减去分子，并且分母保持不变。
添加并减去不同分区的得分，首先是分数，然后减去并减去。
得分规则：使用分子积累作为分子，并使用分母制成分母。
分数分区：除了倒数数至该数字的数量。
单位转换（1）1 km = 1公里1公里= 1000米1米= 10美分1美分= 10 cm 1 cm = 10 mm = 10 mm（2）1平方米= 100平方米的1米1平方米1平方米。
100平方厘米1平方厘米＝100 平方毫米（3）1 立方米＝1000立方分米1000立方厘米1000立方厘米1000立方毫米（4）1000 吨＝1000千克1千克= 1000 = 1 kg = 2磅（5）1公顷= 100,000平方米1英亩= 666.666平方米（6）1升= 1立方米分割仪表= 1 000 ml 1 ml 1 ml = 1立方厘米数量计算方程式1。
单一价格×单一价格×数量×数量 =总价格2。
单收益×数量=总输出3。
速度×时间=距离4。
工作有效×时间=总小学数学定义定理公式（2）1。
添加方法：两个数字添加交换，并且不变。
2。
添加法的组合：添加三个数字，第一个添加前两个数字，或先添加两个数字，然后添加第三个数字并不变。
3。
乘法法：两项计数，即交换因子的位置，不变。
4。
乘法方法：乘以三个数字，首先乘以前两个数字，或者首先乘以两个数字，然后用第三个数字乘。
他们的积累保持不变。
5。
乘法分布定律：两个数字乘以相同的数字，并且两个加上数字可以乘以该数字，并且可以添加两个累积，结果保持不变。
例如：（2+4）×5 = 2×5+4×5.6。
部门的性质：在部门中，部门和部门被扩展（或减少）相同的倍数，业务保持不变。
0除了任何不是0、0.7的数字。
方程：左侧值的值等于右侧的相等值。
平等公式的基本性质：仍然建立了相等公式两侧的相同数量（或分隔）。
8。
公式：包含未知方程式称为方程。
9。
一个美元和一个时间方程：它包含一个未知数，未知数为“等值”形式称为“一个 - 美元方程”。
了解一个 - 美元方程和计算的示例。
也就是说，计算和计算的示例。
10。
分数：将单位“ 1”分为几个副本，表明这种副本或几个分数称为分数。
11。
分数的加法和减法规则：分母的分数并减去分子，并且仅添加并减去分子，并且分母保持不变。
添加并减去不同分区的得分，首先是分数，然后减去并减去。
12。
分数的比较：比较同一分母的得分，分子很大，分子很小。
与不同分区的得分相比，比较点，然后比较； 如果分子相同，则分母很小。
13。
分数成倍增加，并且累积分子乘以得分和整数。
14。
分数乘以乘积，并将分子乘数的累积用作剥夺。
15。
分数除外（除了0除外），该整数等于分数的倒计时乘以该整数。
16。
真正的分数：分子比例的小分数称为真实分数。
17。
假分数：分子得分是大的或分子和划分的。
假分数大于或等于1.18。
乐队得分：将假分数写入整数和真实分数，这称为乐队得分。
19。
分数的基本性质：分子和分母同时乘以或除以相同的数字（0），得分的大小不变。
20。
一个数字分成分数，相当于这个数字的倒计时。
21。
A的个数除以B的个数(0)，等于B的个数除以B的个数。